Article Text
Statistics from Altmetric.com
When clinicians begin their search for the best available evidence to inform decision-making, they are usually directed to the top of the ‘evidence pyramid’ to find out whether a systematic review and meta-analysis have been conducted. The Cochrane Library1 is fast filling with systematic reviews and meta-analyses that aim to answer important clinical questions and provide the most reliable evidence to inform practice and research. So what is meta-analysis and how can it contribute to practice?
What is meta-analysis?
Meta-analysis is a research process used to systematically synthesise or merge the findings of single, independent studies, using statistical methods to calculate an overall or ‘absolute’ effect.2 Meta-analysis does not simply pool data from smaller studies to achieve a larger sample size. Analysts use well recognised, systematic methods to account for differences in sample size, variability (heterogeneity) in study approach and findings (treatment effects) and test how sensitive their results are to their own systematic review protocol (study selection and statistical analysis).2 ,3
The Five-step process
There is debate about the best practice for meta-analysis, however there are five common steps.
Step 1: the research question
A clinical research question is identified and a hypothesis proposed. The likely clinical significance is explained and the study design and analytical plan are justified.
Step 2: systematic review
A systematic review (SR) is specifically designed to address the research question and conducted to identify all studies considered to be both relevant and of sufficiently good quality to warrant inclusion. Often, only studies published in established journals are identified, but identification of ‘unpublished’ data is important to avoid ‘publication bias’ or exclusion of studies with negative findings.4 Some meta-analyses only consider randomised control trials (RCTs) in the quest for highest quality evidence. Other types of ‘experimental’ and ‘quasi-experimental’ studies may be included if they satisfy the defined inclusion/exclusion criteria.
Step 3: data extraction
Once studies are selected for inclusion in the meta-analysis, summary data or outcomes are extracted from each study. In addition, sample sizes and measures of data variability for both intervention and control groups are required. Depending on the study and the research question, outcome measures could include numerical measures or categorical measures. For example, differences in scores on a questionnaire or differences in a measurement level such as blood pressure would be reported as a numerical mean. However, differences in the likelihood of being in one category versus another (eg, vaginal birth versus cesarean birth) are usually reported in terms of risk measures such as OR or relative risk (RR).
Step 4: standardisation and weighting studies
Having assembled all the necessary data, the fourth step is to calculate appropriate summary measures from each study for further analysis. These measures are usually called Effect Sizes and represent the difference in average scores between intervention and control groups. For example, the difference in change in blood pressure between study participants who used drug X compared with participants who used a placebo. Since units of measurement typically vary across included studies, they usually need to be ‘standardised’ in order to produce comparable estimates of this effect. When different outcome measures are used, such as when researchers use different tests, standardisation is imperative. Standardisation is achieved by taking, for each study, the mean score for the intervention group, subtracting the mean for the control group and dividing this result by the appropriate measure of variability in that data set.
The results of some studies need to carry more weight than others. Larger studies (as measured by sample sizes) are thought to produce more precise effect size estimates than smaller studies. Second, studies with less data variability, for example, smaller SD or narrower CIs are often regarded as ‘better quality’ in study design. A weighting statistic that seeks to incorporate both these factors, known as inverse variance, is commonly used.
Step 5: final estimates of effect
The final stage is to select and apply an appropriate model to compare Effect Sizes across different studies. The most common models used are Fixed Effects and Random Effects models. Fixed Effects models are based on the ‘assumption that every study is evaluating a common treatment effect’.5 This means that the assumption is that all studies would estimate the same Effect Size were it not for different levels of sample variability across different studies. In contrast, the Random Effects model ‘assumes that the true treatment effects in the individual studies may be different from each other’.5 and attempts to allow for this additional source of interstudy variation in Effect Sizes. Whether this latter source of variability is likely to be important is often assessed within the meta-analysis by testing for ‘heterogeneity’.
Forest plot
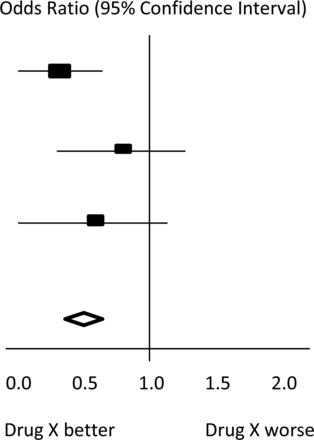
The final estimates from a meta-analysis are often graphically reported in the form of a ‘Forest Plot’.
In the hypothetical Forest Plot shown in figure 1, for each study, a horizontal line indicates the standardised Effect Size estimate (the rectangular box in the centre of each line) and 95% CI for the risk ratio used. For each of the studies, drug X reduced the risk of death (the risk ratio is less than 1.0). However, the first study was larger than the other two (the size of the boxes represents the relative weights calculated by the meta-analysis). Perhaps, because of this, the estimates for the two smaller studies were not statistically significant (the lines emanating from their boxes include the value of 1). When all the three studies were combined in the meta-analysis, as represented by the diamond, we get a more precise estimate of the effect of the drug, where the diamond represents both the combined risk ratio estimate and the limits of the 95% CI.
Hypothetical Forest Plot
Relevance to practice and research
Many Evidence Based Nursing commentaries feature recently published systematic review and meta-analysis because they not only bring new insight or strength to recommendations about the most effective healthcare practices but they also identify where future research should be directed to bridge the gaps or limitations in current evidence. The strength of conclusions from meta-analysis largely depends on the quality of the data available for synthesis. This reflects the quality of individual studies and the systematic review. Meta-analysis does not magically resolve the problem of underpowered or poorly designed studies and clinicians can be frustrated to find that even when a meta-analysis has been conducted, all that the researchers can conclude is that the evidence is weak, there is uncertainty about the effects of treatment and that higher quality research is needed to better inform practice. This is still an important finding and can inform our practice and challenge us to fill the evidence gaps with better quality research in the future.
Footnotes
-
Competing interests None.